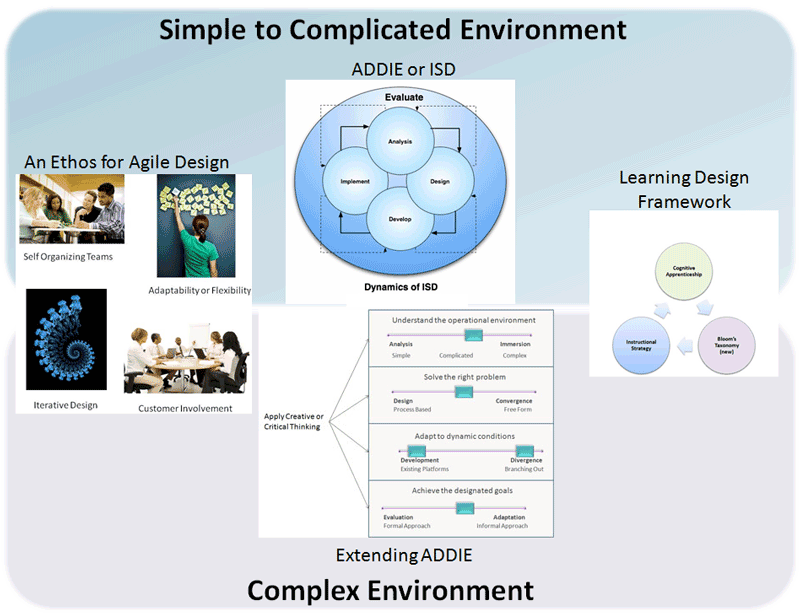
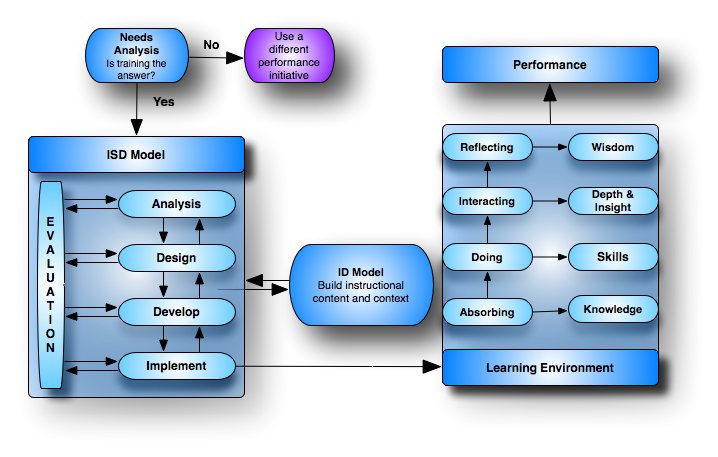
Test Item Analysis
One of the tools used in the evaluation process is an item analysis. It is used to "Test the Test". It ensures testing instruments measure the required behaviors needed by the learners to perform a task to standard. When evaluating tests we need to ask the question: Do the scores on the test provide information that is really useful and accurate in evaluating student performance? The item analysis provides information about the reliability and validity of test items and learner performance. Item Analysis has two purposes: First, to identify defective test items and secondly, to pinpoint the learning materials (content) the learners have and have not mastered, particularly what skills they lack and what material still causes them difficulty (Brown & Frederick, 1971).
NOTE: With the large and normally distributed samples used in the development of standardized tests, it is customary to work with the upper and lower 27 percent of the criterion distribution. Many of the tables used for the computation of item validity indices are based on the assumption that the "27 percent rule" has been followed. Also, if the total sample contains 370 cases, the U and L groups will each include exactly 100 cases, thus preventing the necessity of computing percentages. For this reason it is desirable in a large test item analysis to use a sample of 370 persons.
Because item analysis is often done with small classroom size groups, a simple procedure will be used here. This simple analysis uses a percentage of 33 percent to divide the class in three groups, Upper (U), Middle (M), and Lower (L). An example will be used for this discussion. In a class of 30 students we have chosen 10 students (33 percent) with the highest scores and 10 students (33 percent) with the lowest scores. We now have three groups: U, M, and L. The test has 10 items in it.
Next, we tally the correct responses to each item given by the students in the three groups. This can easily be done by listing the item numbers in one column and prepare three other columns, named U, M, L. As we go through each student's paper, we place a tally mark next to each item that was answered correctly. This is done for each of the ten test papers in the U group, then each of the ten test papers in the M group, and finally for each of the ten papers in the L group. The tallies are then counted and recorded for each group as shown in the table below.
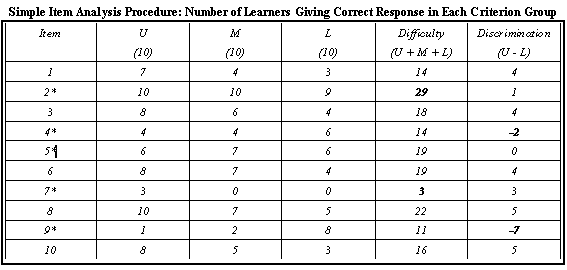
A measure of item Difficulty is obtained by adding the number passing each item in all three criterion groups (U + M + L) as shown in the fifth column. A rough index of the validity or discriminative value of each item is found by subtracting the number of persons answering it correctly in the L group from the number answering it correctly in the U group (L - U) as shown in the sixth column.
Reviewing the table reveals five test items (marked with an *) that require closer examination.
- Item 2 show a low difficulty level. It might be too easy, having been passed by 29 out of 30 learners. If the test item is measuring a valid performance standard, then it could still be an excellent test item.
- Item 4 shows a negative value. Apparently, something about the question or one of the distracters confused the U group, since a greater number of them marked it wrong than the L group. Some of the elements to look for are: wording of the question, double negatives, incorrect terms, distracters that could be consider right, or text that differs from the instructional material.
- Item 5 shows a zero discriminative value. A test item of this nature with a good difficulty rating might still be a valid test item, but other factors should be checked. i.e. Was a large number of the U group missing from training when this point was taught? Was the L group given additional training that could also benefit the U group?
- Item 7 show a high difficulty level. The training program should be checked to see if this point was sufficiently covered by the trainers or if a different type of learning presentation should be developed.
- Item 9 shows a negative value. The high value of the negative number probably indicates a test item that was incorrectly keyed.
As you can see, the item analysis identifies deficiencies either in the test or in the instruction. Discussing questionable items with the class is often sufficient to diagnose the problem. In narrowing down the source of difficulty, it is often helpful to carry out further analysis of each test item. The table below shows the number of learners in the three groups who choose each option in answering the particular items. For brevity, only the first three test items are shown. The correct answers are marked with an *.

This analysis could be done with just the items that were chosen for further examination, or the complete test. You might wonder why perform another analysis for the complete test if most of the test items proved valid in the first one. The answer is to see how well the distracters performed their job. To illustrate this, look at the distracters chosen for item 1. Although the first analysis showed this the be a valid test item, of the distracters chosen by the learners, only A and B we used. Nine learners choose distracter B, seven learners choose distracter C, while none choose distracter D. This distracter needs to be made more realistic or eliminated from the test item. This type of analysis helps us to further refine the testing instrument.
Next Steps
Return to the Table of Contents
References
Brown, Frederick G (1971). Measurement and Evaluation. Itasca, Illinois: F.E. Peacock.
Kelly, T. L. (1939). The Selection of Upper and Lower Groups for the Validation of Test Items. Journal of Educational Psychology. Vol. 30, p.p. 17-24